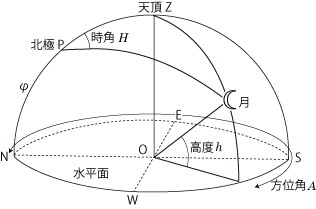
月だけに適用される高度・方位角についての計算式がある訳ではない.しかし夜空を見上げて,まず目につくのは月であり,その位置を確かめたいと思うであろう.年表の掲載値を用いてこれを求めてみよう.
見上げる夜空をO点を中心とした半球と思えば,高度 h,北から東まわりに測った方位角 A は,
で求められる.
ここで,t ≡ 高度・方位角を求める時刻 − 9時 (世界時と中央標準時の差), θ0 ≡ グリニジ視恒星時 (年表:世界時 0hのグリニジ視恒星時のページ参照), (λ, φ) ≡ あなたのいる場所の経度 (東経を+)・緯度,( α, δ ) ≡ 月の赤経・赤緯 (年表:太陽,月のページ参照) とすれば時角 H = θ0 + 1.0027379t + λ − α となる. 1.0027379 は太陽時の恒星時への補正値である.
さて,東京(λ = 139°45′ ≡ 9h19m,φ = 35° 39′ )で1993年1月31日の上弦の月について高度・方位角を求めてみよう.まず,年表:太陽,月によって月の出入の時刻を確かめてみる.月の出は10時41分だから昼間から月は出ていることになる.南中は17時49分,真南の空に見えるはずである.時刻を18時とすれば,月の赤経・赤緯を1月31日と2月1日の値から比例配分で求めて,
1時間は角度に直すと15度にあたるから電卓などで三角関数の値を求めると
ただちに,式(3)から sin h = 0.9589, h = 73.5°
式(1)÷式(2)から tan A = 0.1466

明らかに月は真南から西に動いているから180度を加えて A = 180° + 8.3° = 188.3°
同様に,t = 24h − 9h とすれば h = 11.6°,A = 286.3°となって,2月1日午前0時西の山際にかかる月を見ることになる.そして午前1時3分月入.ちなみに,同日の2時間おきの値を示すと下の表のようになる.
概算値との差は1度以内におさまっているが,特に高度の低いときに違いが大きい.これは月が地球に十分近いために,地心から見た月の赤経・赤緯と観測者から見た月の赤経・赤緯が大きく異なるためで,これを地心視差と呼んでいる.
| 時刻 | 17h49m (南中) | 18h00m | 20h00m | 22h00m | 24h00m | 1h03m (月入) |
|---|---|---|---|---|---|---|
| 方位角 (A) | 179.70° | 188.61° | 248.45° | 270.46° | 286.30° | 294.82° |
| 高度 (h) | 73.47° | 73.33° | 57.49° | 34.24° | 10.97° | -0.55° |
暦象年表1993より加筆、訂正